第一章 绪论
1.1图像压缩概述
随着科学技术的不断发展，日常生活中使用语音、电话、图像、视频等业务在飞速上涨，一方面为生活带来了方便，另一方面，多媒体业务的剧增对有限的频谱资源带来了严峻的挑战，图像压缩技术是一种降低业务数据量的可行方法之一。
数字化图像在制作、存储、复制、传输等方面具有很大的优点，但值得我们注意的是，数字化图像的数据量非常庞大。例如，彩色图像的一个像素内存是3字节，一张普通彩色照片的大小即为680*750*3byte=1.53M.在生活中我们经常传输上百张以上的图片，如果不压缩直接传输将是异常的费时费力。
大数据量的图像信息会给储存器的储存容量，通信干线信道的带宽，以及计算机的处理速度增加极大地压力。单纯靠增加储存容量、提高信道带宽以及计算机处理速度等方法来解决这个问题是跟不上需求的，因此就需要对图像进行压缩处理。
图像数据压缩的可能性是因为图像像素之间，行或者帧之间都存在着较强的相关性。从信息论的角度来看，压缩就是去掉信息中的冗余，即保留确定的信息，去掉不确定的信息（可推知的），也就是用一种更接近信息本质的描述来代替原冗余的描述。一个好的压缩编码方案就是能够最大限度地去除图像中的冗余信息。另外，由于图像最终是由人眼（或通过观测器）来观看的，根据视觉生理、心理特征，可以允许图像经过解码以后有一定的失真，只要这种失真为一般观众难以察觉，或者能够接受。总之，图像压缩编码利用图像的固有统计特性（信源特征），以及视觉生理，心理学特征（信宿特征），或者记录设备和显示设备（如电视监视器）等的特征，从原始图像中经过压缩编码提取有效的信息，尽量去除无用的或者用处不大的冗余信息，一边高效率地进行图像的数字传输或储存，而在复原时仍能够获得与原始图像相差不多的复原图像。
一个压缩编码方法优劣主要由三个重要指标来衡量：1.压缩比要高，有几倍，几十倍，也有几百倍乃至几千倍；2.压缩与解压缩要快，算法要简单，硬件实现 容易；3.解压获得的图像质量要好。在进行图像压缩编码的时候，人们总是希望选择压缩比大，恢复效果好且快速的算法。实际研究表明，图像数据实际被压缩多少，不但取决于所采用的方法，而且与给定图像的结构、分布、相关性和特征匹配等因素有关。为了使压缩方法更为有效，应首先了解原始图像的性质，然后选择合适的方法。
1.2 神经网络概述
1.2.1 神经网络的主要特点特点
神经网络的一般特点可以概括为以下几个方面。
1.自学习和自适应性
自适应性是指一个系统能够改变自身的性能以适应环境变化的能力。当环境变化时，相当于给神经网络输入新的训练样本，网络能够自动调整结构参数，改变映射关系，从而对特定的输入产生相应的期望输出。
2.分布式储存
由于神经元之间的相对独立特性，神经网络学习的“知识”不是集中储存在网络中的某一处，而是分布在网络的所有连接权值中。
1.2.2 BP神经网络
BP神经网络是一种多层前向型神经网络，某神经元的传递是S型函数，输出量为
的连续量，它可以实现从输入到输出的任意非线性映射。由于权值的挑中采用反向传播（Back Propagation）学习算法，因此也常称为BP网络。
目前，在人工神经网络的实际应用中，绝大部分的神经网络模型都采用BP网络及其变化形式。他也是前向型网络的核心部分。BP神经网络主要用于以下四个方面。
1.函数逼近：用输入向量和相应的输出向量训练一个网络逼近函数。
2.模式识别：用一个待定的输出向量将它与输入向量联系起来。
3.分类：把输入向量所定义的合适方式进行分类。
4.数据压缩：减少输出向量维数以便于传输或储存
。
第二章 BP神经网络与图像压缩
2.1 网络结构
BP神经网络一般是多层的，与之相关的另一概念是多层感知器（Multi-Layer Perceptron,MLP）.多层感知器除了输入层和输出层以外，还具有若干个隐含层。多层感知器强调神经网络在结构上由多层组成，BP神经网络则强调网络采用误差反向传播的学习算法。大部分情况下多层感知器采用误差反向传播的算法进行权值调整，因此两者一般指的是同一网络。
BP神经网络的隐含层可以为一层或多层。一个包含2层隐含层的BP神经网络的拓扑结构如图2.1所示：
图2.1 BP神经网络的结构
从上图中的2个隐含层BP神经网络可以发现，BP神经网络有以下特点：
(1) 网络由多层构成，层与层之间全连接，同一层之间的神经元无连接。多层的网络设计，是BP神经网络能够从输入中挖掘更多的信息，完成更复杂的任务。
(2) BP网络的传递函数必须可微。因此，感知器的传输函数——二值函数不能用。BP网络一般使用Sigmoid函数或线性函数作为传递函数。根据输出值是否包含负值，Sigmoid函数又可分为Log-Sigmoid函数和Tam-Sigmoid函数。一个简单的Log-Sigmoid函数可由下式确定：
（2.1）
其中x的范围包含整个实数域，函数值在0到1之间，具体应用时可以增加参数，以控制曲线的位置和形状。
(3) 采用误差反向传播算法（Back-Propagation Algorithm）进行学习。在BP神经网络中，数据从输入层经隐含层逐层向前修正网络的权值连接。随着学习的不断进行，最终的误差越来越小 
。
2.2 BP网络学习算法
确定BP网络的层数和每层的神经元个数以后，还需要确定各层之间的权值系数才能根据输入给出正确的输出值。BP网络的学习属于有监督学习，还需要一组已知目标输出的学习样本集。训练时先使用随机值作为权值，输入学习样本得到网络的输出。然后根据输出值与目标输出计算误差，再由误差根据某种准则逐层修改权值，使误差减小。如此反复，直到误差不再下降，网络训练就完成了。
修改权值有不同的规则。标准的BP神经网络沿着误差性能函数梯度的反方向修改权值，原理与LMS算法比较类似，属于最速下降法。下面介绍两种BP神经网络的学习算法。
1.最速下降BP法
（1）变量定义：在三层BP网络中，假设输入神经元个数为M，隐含神经元个数为I，输入层神经元个数为J。输出层第m个神经元记为
，隐含层第i个神经元记为
，输出层第j个神经元记为
。从
到
的连接权值为
，从
到
的连接权值为
。隐含层传递函数为Sigmoid 函数，输出层传递函数为线性函数。
上述网络接受一个长为M的向量作为输入，最终输出一个长为J的向量。用
和
分别表示每一层的输入与输出，如
表示第I层（即隐含层）第一个神经元的输入。网络的实际输出为：
（2.2）
网络的期望输出为：
（2.3）
n为迭代次数。第n次迭代的误差信号定义为：
（2.4）
将误差能量定义为：
（2.5）
（2）工作信号正向传播
输入层的输出等于整个网络的输入信号：
隐含层第i个神经元的输入等于
的加权和：
（2.6）
假设
的Sigmoid函数，则隐含层第i个神经元的输出等于：
（2.8）
输出层第j个神经元的输入等于
的加权和：
（2.9）
输出层第j个神经元的输出等于：
（2.10）
输出层第j个神经元的误差为：
（2.11）
网络的总误差：
（2.12）
（3）误差信号反向传播
在权值调整阶段，沿着网络逐层反向进行调整，具体步骤如下：
首先调整隐含层与输出层之间的权值
，根据最速下降法，应计算误差对
的梯度
，再沿着该方向反方向进行调整如下所示：
（2.13）
（2.14）
梯度可由求偏导得到。根据微分的链式规则，有：
（2.15）
由于
是
的二次函数，其微分为一次函数：
（2.16）
（2.17）
输出传递层函数的导数：
（2.18）
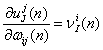（2.19）
因此，梯度值为：
（2.20）
权值修正量为：
（2.21）
引入局部梯度的定义：
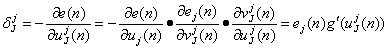（2.22）
因此，权值修正量可表示为：
（2.23）
局部梯度指明权值所需要的变化。神经元局部梯度等于该神经元的误差信号与传递函数导数的乘积。在输出层，传递函数一般为线性函数，因此其导数为1，即：
（2.24）
代入上式，可得：
（2.25）
输出神经元的权值修正相对简单。
误差信号向前传播，对输入层与隐含层之间的权值
进行调整。与上一步类似，应有：
（2.26）
为输入神经元的输出
。
为局部梯度，定义为：
（2.27）
为Sigmoid传递函数。由于隐含层不可见，因此无法直接求解误差对于该层输出值的偏导数
。这里需要使用上一步计算中求得的输出层节点的局部梯度：
（2.28）
故有：
（2.29）
至此，三层BP网络的一轮权值调整的过程就完成了。调整的规则可以总结为：权值调整量
。
当输出层传递函数为线性函数时，输出层与隐含层之间权值调整的规则类似于线性神经网络的权值调整规则。BP网络的复杂之处在于，隐含层与隐含层之间、隐含层与输入层之间调整权值时，局部梯度的计算要用到上一步计算的结果。前一层的局部梯度是最后一层局部梯度的加权和。也正是因为这个原因，BP网络学习权值时只能从后向前依次计算。
2.LM(levenberg-marquardt)算法
LM算法是为了在以近似二阶训练速率进行修正时避免计算Hessian矩阵而设计的。当误差性能函数具有平方和误差（训练前向型网络的典型误差函数）的形式时，Hessian矩阵可以近似表示为：
（2.30）
梯度的计算表达式为：
（2.31）
式中H——包含网络误差函数对权值和阈值一阶导数的雅可比矩阵；
e——网络的误差向量。
雅可比矩阵可以通过标准的前向型网络技术进行计算，比Hessian矩阵的计算要简单。类似于牛顿法，LM算法对上述近似Hessian矩阵按如下形式进行修正：
（2.32）
当系数
为0时，上式即为牛顿法；当系数
的值很大时，上式变为步长较小的梯度下降法。牛顿法逼近最小误差的速度更快，更精确，因此因尽可能的使算法接近于牛顿法，在每一步成功的迭代后（误差性能减小），使
减小；仅在进行尝试迭代后误差性能增加的情况下，才使
增加。这样，该算法每一步迭代的误差性能总是减小的。
LM算法是为了训练中等规模的前馈神经网络（多达数百个连接权）而提出的最快速算法，它对MATLAB实现也是相当有效的，因为其矩阵的计算在MATLAB中是以函数实现的，其属性在设置时变得非常明确。本文的基于BP神经网络算法就是采用的LM算法。
2.3 网络训练
给定一个训练集，修正权值的方式有两种：串行方式和批量方式。工作信号正向传播，根据得到的实际输出计算误差，再次反向修正各层权值。因此
串行方式，反向传播算法的串行学习又可称为在线方式、递增方式或随机方式。网络每获得一个新样本，就计算一次误差并计算权值，直到样本输入完毕。
在串行方式中，每个样本依次输入，需要的储存空间更少。训练样本的选择是随机的，可以降低网络陷入局部最优的可能性。
2.4 图像压缩
1.像压缩编码的可能性
图像压缩编码的理论基础是信息论。从信息论角度来看，压缩就是去掉信息中的冗余，即保留不确定的信息，去掉确定的信息（可推知的），也就是用一种更接近信息本质的描述来代替原有冗余的描述。一幅图像存在着大量的数据冗余和主观视觉冗余，因此图像数据压缩既是必要的，又是可能的。
2.应用环境允许图像有一定的程度失真
（1）接收端图像设备分辨率较低，则可降低图像分辨率。
（2）用户所关心的图像区域有限，可对其余部分图像采用空间和灰度级上的粗化。
（3）根据人的视觉特性对不敏感区域进行将分辨率编码（视觉冗余）。
可以利用视觉的这一特性编码去除人眼的视觉冗余。通常人眼能够分辨的灰度级有限，同时，人眼所感受的图像区域物体的亮度不仅仅与物体的反射光有关，还具有马赫带效应、同时对比度、视觉暂留以及视觉非线性等特点，有些信息在通常的视觉感知过程中并不那么重要，这些信息可被认为是视觉冗余，去除这些冗余，人眼是不能够明显感觉到图像质量的降低，视觉冗余也给图像压缩提供了可能。
2.5 数字图像压缩编码基础
2.5.1 图像压缩的基本概念
1. 信息相关
在绝大多数图像的像素之间，各像素之间，各像素行和帧之间存在着较强的的相关性。从统计观点出发，就是每个像素的灰度值（或颜色值），总是和其周围的其它像素的灰度值（或颜色值）存在某种关系，应用某种编码方法减少这些相关性就可实现图像压缩。
2. 信息冗余
从信息论的角度来看，压缩就是去掉信息中的冗余。即保留确定信息，去掉可推知的确定信息，用一种更接近信息本质的描述来代替原有的冗余描述。
当一幅图像的灰度级别直接用自然二进制编码来表示时，通常会存在冗余。大多数的图像数据存在着不同程度的编码冗余、像素之间的冗余和心理视觉冗余。
由于大多数图像的直方图不是均匀（水平）的，所以图像中某个（或某些）灰度级会比其他灰度级具有更大的出现概率，如果对出现概率大和出现概率小的灰度级都分配相同的比特数，必定会产生编码冗余。更一般的讲，当被赋予事件集的编码（比如灰度级值）如果没有充分利用各种结果出现的概率时，就会出现编码冗余。
所谓像“素间的冗余”，是指单个像素携带的信息相对较少，单一像素对于一幅图像的多数视觉贡献是多余的，它的值可以通过与其相邻的像素的值来推断。这种反映像素间的依赖性的“素间的冗余”通常是空间冗余、几何冗余和帧间冗余的统称。
对于以改善视觉效果为目的的某些应用来说，用户通常允许图像有一定程度的失真；对于以特征提取和目标识别为目的的某些应用来说，用户通常关心的是那些边缘和轮廓信息，允许丢掉与其无关的信息。心里视觉冗余是指在正常的视觉处理过程中那些不十分重要的信息。心里视觉的产生是因为人类对图像信息的感知并不涉及对图像中每个像素值的定量分析。通常，观察者寻找可区别的特征，比如边缘或者文理区域，然后在心里将其合并成可识别的组群，最后，通过大脑将这些组群与先前已有的知识相联系以便完成图像的解释过程。
3. 信源编码及其分类
图像压缩的目的是在满足一定的图像质量条件下，用尽可能少的比特数来表示原图像，以减少图像的存储容量和提高图像的传输效率。在信息论中，把这种高通过减少冗余数据来实现数据压缩的过程称为信源编码。信源编码分为无失编码和有失真编码两大类。无失真压缩用无失真编码方法实现，有失真压缩用有时真编码方法来实现。无失真压缩也称为无损压缩，是一种在不引入任何失真的条件下使表示图像的数据比特率为最小的压缩方法。无损压缩是可逆的，即从压缩后的图像能够完全恢复出原图像而没有任何信息损失。
有失真压缩也称为有损压缩方法，是一种在一定比特率下获得最佳保真度，或在给定的保真度下获得最小比特率的压缩方法。由于有损压缩有一定的信息损失，所以是不可逆的，即无法从压缩后的图像恢复出原图像
。
2.5.2 图像编码模型
1. 图像编码系统模型
图像编码的主要目的是图像数据的压缩，所以一个完整的图像编码系统模型主要由通过信道连接的编码器和解码器组成，如图2.5所示。
图2.5 图像编码系统模型
编码器的输入是原图像
,输出是编码器产生的一组符号。这组符号经过信道传输后，作为解码器的输入进入解码器，解码器的输出是解码重建的图像
。
编码器由一个用于消除输入冗余的信源编码器和一个用于增强信源编码器输出的抗干扰、抗噪声能力的信道编码器组成。与编码器相对应，解码器由一个信道解码器和一个信源解码器组成。如果连接编码器和解码器之间的信道是无干扰和无噪声的，则在符号的传输过程中就不会产生误差，信道编码器和信道解码器就都可以不要，这是编码器和解码器就分别只由信源编码器和信源解码器祖成。
信道是连接信息源和用户的物理媒介。信道可以是电话线、电缆、电磁能量传输路径或数字电子计算机中的数据线。
2. 信道编码器和信道解码器
信道编码器和信道解码器是一种用来实现抗干扰、抗噪声的可靠数字通信技术措施，当传输信道是有噪声的或易产生错误时，信道编码器和信道解码器就会在整个编解码处理和信息传输过程中起到十分重要的作用。信道编码器是通过向信源编码数据中插入可控制的冗余数据来减少对信道噪声的影响的。
3. 信源编码器模型和信源解码器模型
在信息论中，把通过减少冗余来压缩数据的过程称为信源编码。显然，信源编码器的作用就是减少或消除输入图像中的编码冗余。特定的应用和与之联系的保真度要求规定了在给定条件下所使用的编码方法。具体信源编码器模型如图2.6所示：
对于图2.7所示的信源解码器来说，其操作次序、原理及其功能正好与信源编码器相反。
2.6 图像压缩编码的评价标准
2.6.1 信息熵
信息消息的不确定度量，消息的可能性越小，其蕴含的信息量就越大，即不确定性程度越大；反之，消息的可能性越大，其信息越少，即不确定性越小。假设从N个数中选中某个数x的概率为P（x），则根据Shannon（香农）理论，定义其信息为
：
（2.33）
如果将信源所有可能事件的信息量进行平均，就得到信息熵（entropy）,所谓熵就是平均信息量。
信源x的符号集为
，设出现的概率为
，则信息x的熵为
（2.34）
根据Shannon（香农）无噪声编码定理，对于熵为H的信号源，对其无失真编码，所能达到的最大值为
/每符号，这里
为一任意小的正数，因此可能达到的最大压缩比为：
（2.35）
方均信噪比为：
（2.36）
均方根信噪比为：
（2.37）
2.6.2 评价标准
在图像压缩编码中，解码图像与原始图像可能会有差异，因此，需要评价压缩后图像的质量。描述解码图像相对于原始图像偏离程度的测度一般称其为保真度（逼真度）准则。常用的准则可分为客观保真度准则以及主观保真度准则两大类。
1.客观保真度准则
最初常用的客观保真度准则是原始图像和解码图像之间的方均根误差和方均根信噪比两种。令
代表原始图像，代表对
先压缩在解压后得到的
的近似，对任意x和y，
和之间的误差
定义为：
（2.38）
若f(x,y)和 均为M x N ,则他们之间的方均根误差为：
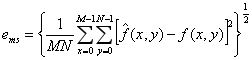（2.39）
如果将
看做原始图像
噪声信号
的和那么解压图像的方均根信噪比 
为
（2.40）
如果对上面的式子求平方根，就得到了方均根信噪比
。实际使用中常将
归一化并用分贝（dB)表示，令
（2.41）
则有
（2.42）
如果令
（其中，
）则可能得到峰值信噪比PSNR：
（2.43）
2. 主观保真度准则
尽管客观保真度准则提供了一种简单、方便的评估信息损失的方法，但很多解压缩图像最终是供人观看的。事实上，具有相同客观保真度的不同图像，对人的视觉可能产生不同的视觉效果。这是因为客观保真度准则是一种统计平均意义下的度量准则，它对于图像中的细节无法反映出来。而人的视觉系统却具有独特的特性，能够察觉出来。在这种情况下，用主观的方法来谢亮图像的质量更为合适。一种常用的方法是对一组（不少于20人）观察者显示图像，并将它们对该图像的评分取平均，用来评价一幅图像的主管质量
。
2.7 基于小波变换的图像压缩编码
小波变换是在短时傅里叶变换的基础上发展起来的一种新型变换方法，他是一种时—频分析法，具有多分辨率分析（Multiresolution Analysis）的特点，而且在时、频域都具有表征信号局部特征的能力，是一种窗口大小不变、形状可变、时间窗和频率窗都可以改变的时频局部化分析方法。小波变换由于具有很好的时—频特性而且可以匹配人类视觉系统的特性，因而得到图像压缩编码领域的极大关注。
小波分析在图像领域的应用应归功于Mallat。1987年，Mallat巧妙地将计算机视觉领域内的多尺度分析思想引入到小波分析中小波函数的构造，从而统一了在此之前的各种小波的构造方法。Mallat研究了小波变换的离散形式，并将相应的算法应用于图像的分解与重建，为随后的小波图像压缩奠定了基础。进入90年代，利用小波进行图像压缩的研究得到了空前的关注。这一时期正是互联网蓬勃兴起的时候，因此如何适应网络的特点进行图像编码得到了重视。1993年，Shapiro首先将零树的概念引入到小波图像压缩中，这种称为EZW的方法可以对图像进行渐进性编码，具有很高的压缩性能，非常适合于网络图像的传输与浏览。对于图像来说，如果需要进行快速或实时传输以及大量存储，就需要对图像数据进行压缩。在同样的通信容量下，如果图像数据压缩后再传输，就可以传输更多的图像信息。例如，用普通的电话线传输图像信息。图像压缩研究的就是寻找高压缩比的方法且压缩后的图像要有合适的信噪比,在压缩传输后还要恢复原信号，并且在压缩、传输、恢复的过程中，还要求图像的失真度小，这就是图像压缩的研究问题。图像数据往往存在各种信息的冗余、如空间冗余、信息熵冗余、视觉冗余和结构冗余等等。所谓压缩就是去掉各种冗余，保留对我们有用的信息。图像压缩的过程常称为编码。相对的，图像的恢复就是解码。图像压缩的方法通常可分为有失真编码和无失真编码两大类：无失真编码方法如改进的霍夫曼编码。有失真编码方法的还原图像较之原始图像存在着一些误差，但视觉效果是可以接受的。常见的方法有预测编码、变换编码、量化编码、信息熵编码、分频带编码和结构编码等。
在小波分析中也有两个重要的数学实体：“积分小波变换”和“小波级数”。积分小波变换是基小波的某个函数的反射膨胀卷积，而小波级数是称为小波基的一个函数，用两种很简单的运算“二进制膨胀”与“整数平移”表示。通过这种膨胀和平移运算可以对信号进行多尺度的细致表示。通过这种膨胀和平移运算可以对信号进行多尺度的细致的动态分析，从而能够解决Fourier变换不能解决的许多困难问题。利用小波变换可以一次变换整幅图像，不仅可以达到很高的压缩比，而且会出现JPEG重建图像中的“方块”效应，但编码器复杂，有潜像问题。
由于小波及小波包技术可以将信号或图像分层次按小波基展开，所以可以根据图像信号的性质以及事先给定的图像处理要求确定到底要展开到哪一级为止，从而不仅能有效地控制计算量，满足实时处理的需要，而且可以方便地实现通常由子频带、层次编码技术实现的累进传输编码（即采取逐步浮现的方式传送多媒体图像）。这样一种工作方式在多媒体数据浏览、医学图片远程诊断时是非常必要的。另外，利用小波变换具有放大、缩小和平移的数学显微镜的功能，可以方便地产生各种分辨率的图像，从而适应于不同分辨率的图像I/O设备和不同传输速率的通信系统。相比之下，利用KL变换进行压缩编码，只能对整幅图像进行；而利用小波变换则能够比较精确地进行图像拼接，因此对较大的图像可以进行分块处理，然后再进行拼接。显然，这种处理方式为图像的并行处理提供了理论依据
。
第三章 
基于BP神经网络的图像压缩编码
利用BP神经网络做图像压缩和解压缩的过程如图3.1所示：
其中，熵编码过程针对神经网络压缩的输出进行，进一步去除统计冗余。
3.1 压缩步骤
1. 图像块划分
简单起见，这里将所有输入图像的大小调整为128*128像素大小。为了控制神经网络规模，规定网络输入神经元节点个数为16个，即将图像划分为1024个4*4大小的图像块，将每个图像块作为一个样本向量，保存为16*1024大小的样矩阵，如图3.2所示：
图3.2 图像块的划分
归一化。神经网络的输入样本一般都需要进行归一化处理，这样能够保证性能的稳定性。归一化可使用 mapminmax 函数进行，考虑到图像数据的特殊性，像素点灰度值为整数，且处于0到255之间，因此归一化处理统一将数据除以255即可。例如，读入一幅图像，进行归一化处理：
>>I=imread(‘lena.bmp’);
>>imshow(I);
>>I0=double(I)/255;%归一化处理
>>[min(I0(:)),max(I0(:))]
ans=
0.0745 0.9608
可见，归一化后图像的数据处于0.0745到0.0968之间，位于
区间内。这样做还有一个好处，如果使用 mapminmax 函数，需要出巡每一行数据的最大值和最小值，这样最终的压缩数据里必须包含这一部分数据，使得压缩率下降。
2. 建立BP神经网络
采用MATLAB 神经网络工具箱的feedforwardnet 函数创建BP神经网络，并制定训练算法。为了达到较好的效果，采用LM训练法。同时确定目标误差和最大迭代次数。
然后，就可以调用 train 函数进行训练了。
tic 和 toc 用于记录训练时间 
。
如图3.3所示为BP网络训练的界面。从网络训练界面可以看出该网络的基本信息输入层和输出层神经元的个数为4个，隐含层神经元的个数为N=2。Algorithm栏表示是相关参数。Epoch表示训练的次数，500表示最大训练次数，从图中可知，N=2时的真实训练次数为6次；Times表示的是训练时间为15秒；Performance表示的是程序中指定的训练结束参数，只要有一个参数满足条件即结束训练，0.197是初始值，0.001是结束值，即程序里的goal，0.000975是当前迭代时得到的Mean Squared Error（均方误差）；Gradient表示的是误差曲线的梯度；变量mu确定了学习是根据牛顿法还是梯度法来完成。Plots指的是各种曲线，按下每个按钮，即可出现不同的曲线，代表不同的意思。如图3.3a所示，为依次点击三个按钮所得到的图像。点击Performance可以得到训练过程的变化图像，其中Goal表示性能目标，Best表示所能达到的最好状态；点击Traning State按钮，可以对详细的训练状态进行详细的了解，由上而下分别表示误差曲线梯度、mu代表的是函数trainlm中的参数和有效性检查。Error Histogram表示限定误差直方图。点击Regression按钮得到的是依次是训练样本、验证样本、测试样本和全部样本的回归系数啊，越接近于1越好，也就是两根线越接近越好。
图3.3 BP网络的训练界面
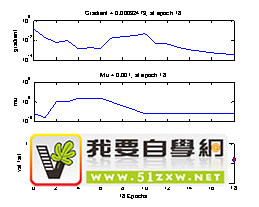
图3.3a训练BP之后的参数
图3.3a训练BP之后的参数
3. 保存结果
训练完成后，压缩的结果是每个输入模式对应的隐含神经元向量的值，一级网络的权值和阈值，以及网络的权值和阈值。将输入模式输入网络，与输入层和隐含层之间的权值矩阵相乘，再用 Sigmoid 函数处理，即可得到隐含神经元的值。
（3-1）
此时得到的结果为浮点数，为了提高压缩效率，将其量化为
比特的整数。方法是先对矩阵进行归一化，使其范围固定在
之间，再乘以
，最后取整即可。
在MATLAB中使用save 命令可将变量保存至文件的命令方式如下：
save comp com minlw maxlw minb maxb mind
3.2 解压缩步骤
1. 加载文件。使用load 命令加载数据文件。
2. 数据反归一化。每一个数据乘以
，得到
之间的小数，再将其映射到数据原区中去。形式如下
：
com.lw=double(com.lw)/63;
com.lw=com.lw*(maxlw-minlw)+minlw;
3. 重建。此时的数据为BP神经网络隐含层的神经元输出值，为了重建图像，需要将其输出到网络中，与隐含层和输出层之间的权重矩阵相乘。
4. 图像反归一化。图像反归一化不需要使用自定义的区间范围，只需将每份数据乘以像素峰值255，并取整即可。
5. 图像恢复。假设划分图像块时，以4*4为单位进行划分，则矩阵应为16*N大小。每一列抽取出来，重新排列为4*4矩阵，并对各个矩阵按行进行排列，即可恢复原图像。
3.3 压缩/解压代仿真结果
本次仿真用的电脑处理器是Intel(R) Core(TM) i5-4200H CPU @ 2.80GHz 2.79GHz；内存4.00GB；64位操作系统。
3.3.1 基于BP神经网络的图像压缩编码仿真结果
1. 首先先对图像进行预处理，之后建立神经网络设置参数，其次使用要进行压缩的图像对神经网络进行训练，使用bp_imageCompress党阀，并调用block_divide函数，实现图像的压缩；最后对图像进行重建，使用bp_imageRecon方法，并调用re_divide函数。具体的源程序见附录。
2. 仿真结果如图3.4所示，此时的隐含层神经元数目为N=8时的原图像和重建图像。同时在命令窗口输入重建图像的峰值信噪比和压缩比率，可以得到此时的压缩的峰值信噪比为PSNR=31.1015，压缩率为rate=25.12%，峰值信噪比较高，但是图像的压缩比比较低。
改变隐含层神经元的个数可以调节峰值信噪比（PSNR）和图像压缩率。下面给出了3次调节隐含层神经元的个数所得到的结果：
图3.4 N=8 仿真结果
当隐含层有16个神经元时，结果如图3.6所示，此时的峰值信噪比（PSNR）为PSNR=29.3982，图像压缩率为rate=46.94%，峰值信噪比略微下降，但是图像压缩比有了较大的提升。
图3.6 N=16时的原图像与重建图像
当隐含层有30个神经元时，结果如图3.7所示，此时的峰值信噪（PSNR）为PSNR=27.7330，图像压缩率为rate=78.47%。
图3.7 N=30时的原图像与重建图像
从以上三次试验的结果可以看出，通过逐渐增加隐含层神经元的个数，图像的压缩比在逐渐的提高。但通过比对每次实验结果中的峰值信噪比PSNR可以发现图像的峰值信噪比在逐渐下降，这说明重建图像的质量也在不断变差。
显然，在图像压缩过程中不能只注重图像的压缩比，还要注意重建图像的质量不能太差。因此，隐含层神经元的个数要进行一定的限定，具体的计算方法如下所示：
（3-2）
其中，
为隐含层神经元的个数，m和n分别表示的是输入层和输出层神经元的个数，a为
之间的常数。因此确定出来的隐含层神经元的个数为一个范围，之后，再进行不断地实验，通过图像的对比，得出在压缩比较高且重建图像质量也较高时的隐含层神经元的个数
。
3.3.2 基于小波变换的图像压缩编码仿真结果
基于小波变换的图像压缩首的具体步骤如下（MATLAB源程序见附录）：
1. 对图像用小波进行分解；
2. 提取小波分解结构中的一层低频系数和高频系数并对各频率成分进行重构；
3. 进行图像进行第一次压缩，保留小波分解第一层低频信息，对第一层信息进行量化编码。提取小波分解结构中的一层低频系数和高频系数；
4. 对矩阵进行伪彩色编码并获取色图；
5. 对第一次压缩后的图像保留小波分解第二层低频信息进行压缩并对其进行量化编码；
6. 改变图像的高度并显示第二次压缩后的压缩图像。
如图3.5所示为小波变换图像压缩编码后的MATLAB仿真结果,通过计算可以得出该图像基于小波变换的图像压缩编码压缩后的压缩比为91.50%，压缩比是比较高的。压缩前后图像的具体数据如表3-1所示：
表3-1 基于小波变换图像压缩后原图像与压缩图像的具体数据
|
Name |
Size |
Bytes |
Class |
Comment |
|
I2 |
256*256 |
524288 |
double |
原始图像 |
|
ca1 |
135*135 |
145800 |
double |
第一次压缩后图像 |
|
ca2 |
7*75 |
45000 |
double |
第二次压缩后图像 |
图3.5 基于小波变换的图像压缩结果
3.4 结果分析
从图3.4中可以看出，由于算法将图像强行分割为4*4的块，并分别进行训练，图像会在某种程度上出现块效应现象，表现为块与块之间的差异较大。
基于小波变换的图像压缩编码经过两次压缩之后的图像压缩比为91.5%，显然比基于BP神经网络的图像压缩编码之后的图像压缩比高出很多，这是因为本次实验使用的是最原始的BP神经网络，通过查阅资料找到解决问题的方法是对BP神经网络进行改进，如对分块进行分类，采用不同的隐含层节点数进行训练等可以显著提高效果。另外，在本次设计过程中省略了熵编码的过程，没有进一步去除统计冗余，也是图像压缩比率不高的原因之一
。
第四章 总结与展望
本文首先介绍了图像压缩编码的背景和图像压缩编码的必要性。之后介绍了图像压缩编码的基础和图像压缩编码的评价标准。基于BP神经网络的图像压缩编码的思路、流程、方法等。最后通过MATLAB编程实现基于BP神经网络的图像压缩编码。通过图像数据预处理、网络建立和训练、仿真、图像重建四个步骤对图像进行压缩处理，然后利用输入与重建图像的信噪比和峰值信噪比两个性能函数来评定图像压缩的质量，当信噪比和峰值信噪比越大时，表明图像压缩质量越好，图像失真较小。并利用压缩比和比特率两个性能函数来评价压缩性能。压缩比较大，并且压缩重建后的图像失真较小，说明该压缩方法性能较好。经过运用两种方法对图像进行压缩实验，我门可以看出，BP 网络算法、小波压缩算法都能比较好的进行图像压缩运算。
其中 BP 网络算法应用比较成熟，而且应用了比较好的训练方法，例如牛顿法，自适应改变学习速率和动量法等训练函数，能够很好 的训练 BP 网络，并且得到了比较理想的压缩重建图像。而 SOFM 网络基于矢量化算法来进行图像压缩编码的，是比较有前景的压缩技术，它们应用较少的聚类中心来表示与其接近相似的模式类别，使原始图像数据得到压缩，运用起来比较方便，并且经过对网络训练调试之后，压缩图像也比较理想。但是比较复杂的图像，两者都得增加竞争层的神经元个数，即牺牲了压缩比，来提高图像重建的质量。因此也存在它的不足之处。
参考文献
[1] 张徳丰，《MATLAB神经网络应用设计》（第二版）机械工业出版社.
[2] 陈明 等著，《MATLAB神经网络原理与实例精解》，清华大学出版社.
[3] 张徳丰，《MATLAB数字图像处理》（第二版）机械工业出版社，
.
[4] 张春田，张静著，《数字图像压缩编码》。清华大学出版社.
[5] 《关于图像压缩编码算法研究的综述》，王向阳，烟台师范学院学报(自然科学版).
[6] 张丽英，提升框架下整数小波变换结合VQ图像压缩方法的研究;吉林大学;2004年.
[7] 陈明，《MATLAB函数功能速查效率手册》电子工业出版社.
[8] 杨晓华，孔令泉《MATLAB权威指南》.机械工业出版社，,2013年第一版
.
[9] 李俊山，李旭辉《数字图像处理》（第二版）清湖大学出版社，
.
[10] 罗强 著，《图像压缩编码方法》。西安电子科技大学出版社.
致 谢
经过几个月的努力，我终于完成了本次毕业设计，对此我首先要感谢我的指导老师关娜老师对我的指导和帮助，关娜老师有着丰富的理论知识，严谨的治学态度，对学生认真负责，不惜花费大量的个人时间帮助学生指导和解决问题。在毕业设计的关键阶段，我遇到了很多知识上的瓶颈，通过自己找资料解决了一部分，但还是有很多问题自己解决不了。从课题选择，到方案设计，到具体程序调试，关老师都给我极大的帮助，让我的毕业设计能够比较顺利的完成。
感谢本科这四年所有教过我的老师，从他们那里，我学得了丰富的专业知识，同时我还要感谢评审组老师在百忙之中抽出时间审阅我的论文和参与我的答辩。
最后，我要感谢母校这四年里对于我的培养，让我掌握了丰富的专业知识，为以后更深层次的学习和工作打下良好的基础。
附录1 外文文献
外文正文：
Digital image compression
Digital image compression, also known as image compression or image coding is divided into still image compression and motion image compression (video compression). There is a high degree of correlation in the image data, an image of internal and video images between a lot of redundant information. Redundant information including the following five:
(1) Time redundancy: the difference between adjacent frames of the image sequence is very small, this time redundancy is called temporal redundancy.
(2) spatial redundancy: an image internal uniform coloring part, or the images within the regular pattern, this space-related redundancy is known as spatial redundancy.
(3) structural redundancy: in strong texture, or between the various parts of the image there is a certain relationship, such as self-similarity in the part of the image area memory. This redundancy is called structural redundancy.
(4) the redundancy of knowledge: The information contained in the image and some basic knowledge of a priori, such as in the general face images, the mutual position of the head, eyes, nose and mouth is some common sense. This redundancy is called knowledge redundancy.
(5) visual redundancy: In most cases, the ultimate recipients of the reconstructed image is the human eye. In order to achieve higher compression ratio, you can use the characteristics of the human visual system. For example, the human eye, the ability to distinguish different colors, the sensitivity of different directions. Therefore, if the encoding scheme is the use of some of the features of the human visual system, can further improve the compression ratio and image of the so-called subjective quality.
Image coding is possible to remove redundant information of the various forms in order to reduce the number of bits representing the image required
Commonly used in image compression methods are the following:
1, the run length encoding (RLE)
Length encoding (run-length encoding) is one of the easiest way to compress a file.
Its approach is a series of duplicate values ??(for example, the gray values ??of image pixels) with a single value plus A count value to replace. For example, there is such a letter sequence aabbbccccccccdddddd the stroke length
Encoding is 2a3b8c6d. This method is very easy to implement, but also for string compression with long repeated values。The coding is very effective. For example, there are large areas of continuous shadow or the image of the same color, using this method pressure。Reduction effect of a good. Many bitmap file formats with a run length encoding, such as TIFF, PCX, GEM.
2, the LZW coding
This is the abbreviation of the name of three inventors (the Lempel, Ziv, Welch), its principle is that each one byte
The value should be paired with the value of the next byte is a character, and set a code for each character. When the same Kind of a character on the re-emergence of code instead of this character pair, then this code and the next Character matching.
LZW coding principle is an important feature, the code is not only able to replace a bunch of the same value of the data, but also be able to replace.A bunch of different data values. If some of the different data values ??in the image data is often repeated, can also be found A code to replace the data string. In this regard, the LZW compression principle is better than RLE.
3, Huffman coding
Huffman coding (Huffman encoding) instead of the original data is not fixed length coding to achieve. Huffman coding was first established, in order to compress the text file and so far has been a lot of change Body. Its basic idea is the frequency the higher the value, the shorter the length of its corresponding coding, on the contrary the frequency of the more Low values, the corresponding coding length.
Huffman coding rarely achieve 8:1 compression ratio, In addition, it also has the following two problems: ① The it must be refined Indeed the statistics of the frequency of occurrence of each value in the original document, if not this precise statistics, the effect of compression on will be greatly reduced, or even less than the compression effect. Huffman coding is usually to go through twice the operation, the first Over the statistics, the second time the code, the encoding process is relatively slow. In addition, due to various length,encoded in the decoding process is relatively complex, so the extraction process is relatively slow. ② it is more sensitive. Huffman coding all together regardless of byte sub, so increase Plus one, or reduce one will make the decoding results beyond recognition.
4, prediction and interpolation coding
Usually in the local region in the image pixels are highly correlated, so using the previous pixel gray Expected degree of knowledge of the current pixel gray, which is forecast. The so-called interpolation is based on previous and pixel gray-scale knowledge to infer the current pixel grayscale. If the prediction and interpolation is correct,Do not have to compress each pixel gray, but the difference between the predicted value and the actual pixel values ??after Entropy coded and sent to the receiving end. Predictive value and the difference signal to reconstruct the original pixel in the receiving end.Predictive coding can be obtained relatively high coding quality, and relatively simple to achieve, which is widely used in image compression coding system. But its compression ratio is not high, and accurate prediction depends on the image special.Of a priori knowledge, and must make a large number of non-linear operation, it is generally not used alone, but used in combination with other methods. Such as predictive coding in JPEG DCT DC coefficient The encoding of the exchange coefficient is used to quantify the + RLE + Huffman coding.
5, vector quantization coding
Vector quantization encoding the high correlation between adjacent image data, the input image data sequence grouping,Each set of m data constitute an m-dimensional vector, is encoded together, that is, to quantify more than once. According to the Shannon rate, Distortion theory for memoryless sources, the vector quantization coding is always better than scalar quantization coding.Before coding, first by the large number of samples of the training or learning, or self-organizing feature map neural network, get A series of standard image mode, each image pattern is called a codeword or code vector, these codewords or code vectors together.Together are called the codebook, the codebook is actually a database. The input image block in accordance with a certain way to form an input Vector. Encoding this input vector and all codewords of the code book to calculate the distance to find the nearest codeword, That is to find the best matching image block. The output index (address) as the encoding results. Decoding process is the opposite.
According to the coding results of the index from the code book to find the index corresponding to code word (the code book and codingCodebook), constitute the decoding result. Therefore, vector quantization coding is a lossy codec. At present the use of more,the multi-vector quantization coding scheme is a random vector quantization, the transform domain vector quantization, finite state vector quantization, the address vector quantization waveform gain vector quantization, classified vector quantization, and prediction vector quantization.
6, transform coding
Transform coding image intensity matrix (time-domain signal) transform to the coefficient space (frequency domain signal) motivated Line processing method. Has a strong signal in space, reflected in the frequency domain within certain areas.The amount is often together, or the distribution of the coefficient matrix with some regularity. We can use these rules,Law to reduce the number of quantization bits in the frequency domain, to achieve the purpose of compression. As the transformation matrix of orthogonal transformation is reversible .Inverse matrix transpose matrix are equal, which makes the decoding operation is the solvability of operator convenience, so the operational matrix of the total is the choice of the orthogonal transform to do.
Commonly used transform coding K-L transform coding and DCT coding. K-L transform coding in compression ratio is superior to DCT coding, but the large amount of computation and there is no fast algorithm for DCT coding is widely used in practical application.
7, the model law coding
Predictive coding, vector quantization coding and transform coding is a waveform coding, its theoretical foundation is a signal processor.Theory and information theory; starting point is the image signal as irregular statistical signal from the correlation between pixels.This image signal statistical model starting the design of the encoder. Model coding is the use of computer vision and computer Graphics analysis and synthesis of knowledge on the image signal.Model coding the image signal as the target and scene projection in the 3D world to the product of the two-dimensional plane, while Evaluation of the product is determined by the characteristics of the human visual system. Model encoded key is a particular graph.Like model, and according to this model to determine the characteristic parameters of the image of the scene, such as motion parameters, shape parameters.And so on. Decoding according to the parameters and known model synthesis image reconstruction of images. Encoded object is a specialSign parameters, instead of the original image, it is possible to achieve relatively large compression ratio. The error introduced by the model coding is less sensitive to the human visual geometric distortion, the reconstructed image is very natural and realistic.
In addition, in recent years, fractal coding coding and wavelet transform techniques and an increasing number of applications in image compression.Reduction of the field, but most are still in the research stage, still in front of the common image compression method described in the main. Of course, in actual applications, a variety of image compression methods are often combined to use, such as JPEG.
附录2 外文翻译
数字图像压缩技术介绍
数字图像压缩又称为图像压缩或图像编码；分为静止图像压缩和运动图像压缩，视频压缩。由于图像数据中存在着高度的相关性，一幅图像内部及视频图、像之间存在大量的冗余信息。这些冗余信息主要包括以下五种：
1.时间冗余：图像序列的相邻帧之间差别很小，这种与时间相关的冗余称为时间冗余。
2.空间冗余：一幅图像内部存在均匀着色的部分，或者图像内部存在规则的模式；这种与空间相关的冗余称为空间冗余。
3.结构冗余：在图像的部分区域内存在着较强的纹理结构，或者图像的各部分之间存在着某种关系。如自相似性，这种冗余称为结构冗余。
4.知识冗余：图像中包含的信息与某些先验的基础知识有关；如在一般的人脸图像中，头、眼、鼻和嘴的相互位置等信息就是一些常识。这种冗余称为知识冗余。
5.视觉冗余：在多数情况下，重建图像的最终接受者是人的眼睛。为了达到较高的压缩比，可以利用人类视觉系统的特点。比如人眼对不同颜色的分辨能力不同，对不同方向的敏感度也不同等等。因此，如果编码方案利用人类视觉的一些特点，可以进一步提高压缩比和图像的所谓主观质量。系统图像编码就是要尽可能的去除上述各种形式的冗余信息，以降低表示图像所需的比特数。
常用的图像的压缩方法有以下几种：
1.行程长度编码RLE，
行程长度编码run-length encoding，是压缩一个文件最简单的方法之一。它的做法就是把一系列的重复值，例如图象像素的灰度值，用一个单独的值再加上一个计数值来取代。比如有这样一个字母序列aabbbccccccccdddddd它的行程长度编码就是2a3b8c6d。这种方法实现起来很容易，而且对于具有长重复值的串的压缩编码很有效。例如对于有大面积的连续阴影或者颜色相同的图象，使用这种方法压缩效果很好。很多位图文件格式都用行程长度编码，例如TIFF；PCX；
GEM等。
2.LZW编码
这是三个发明人名字的缩写Lempel；Ziv；Welch，其原理是将每一个字节的值都要与下一个字节的值配成一个字符对，并为每个字符对设定一个代码。当同样的一个字符对再度出现时，就用代号代替这一字符对，然后再以这个代号与下个字符配对。 LZW编码原理的一个重要特征是，代码不仅仅能取代一串同值的数据，也能够代替一串不同值的数据。在图像数据中若有某些不同值的数据经常重复出现，也能找到一个代号来取代这些数据串。在此方面，LZW压缩原理是优于RLE的。
3.霍夫曼编码
霍夫曼编码Huffman encoding，是通过用不固定长度的编码代替原始数据来实现的。霍夫曼编码最初是为了对文本文件进行压缩而建立的，迄今已经有很多变体。它的基本思路是出现频率越高的值，其对应的编码长度越短，反之出现频率越低的值，其对应的编码长度越长。
霍夫曼编码很少能达到8：1的压缩比，此外它还有以下两个不足：它必须精确地统计出原始文件中每个值的出现频率，如果没有这个精确统计，压缩的效果就会大打折，甚至根本达不到压缩的效果。霍夫曼编码通常要经过两遍操作，第一遍进行统计，第二遍产生编码，所以编码的过程是比较慢的。另外由于各种长度的编码的译码过程也是比较复杂的，因此解压缩的过程也比较慢。它对于位的增删比较敏感。由于霍夫曼编码的所有位都是合在一起的而不考虑字节分位，因此增加一位或者减少一位都会使译码结果面目全非。
4.预测及内插编码
一般在图象中局部区域的象素是高度相关的，因此可以用先前的象素的有关灰度知识来对当前象素的灰度进行预计，这就是预测。而所谓内插就是根据先前的和后来的象素的灰度知识来推断当前象素的灰度情况。如果预测和内插是正确的，则不必对每一个象素的灰度都进行压缩，而是把预测值与实际象素值之间的差值经过熵编码后发送到接收端。在接收端通过预测值加差值信号来重建原像素。
预测编码可以获得比较高的编码质量，并且实现起来比较简单，因而被广泛地应用于图象压缩编码系统。但是它的压缩比并不高，而且精确的预测有赖于图象特性的大量的先验知识，并且必须作大量的非线性运算，因此一般不单独使用，而是与其它方法结合起来使用。如在JPEG中；使用了预测编码技术对DCT直流系数进行编码，而对交流系数则使用量化游程编码或霍夫曼编码。
5.矢量量化编码
矢量量化编码利用相邻图象数据间的高度相关性，将输入图象数据序列分组，每一组m个数据构成一个m维矢量，一起进行编码，即一次量化多个点。根据香农率失真理论，对于无记忆信源，矢量量化编码总是优于标量量化编码。
编码前，先通过大量样本的训练或学习或自组织特征映射神经网络方法，得到一系列的标准图象模式，每一个图象模式就称为码字或码矢，这些码字或码矢合在一起称为码书，码书实际上就是数据库。输入图象块按照一定的方式形成一个输入矢量。编码时用这个输入矢量与码书中的所有码字计算距离，找到距离最近的码字，即找到最佳匹配图象块。输出其索引地址，作为编码结果。解码过程与之相反，根据编码结果中的索引从码书中找到索引对应的码字，该码书必须与编码时使用的码书一致，构成解码结果。由此可知，矢量量化编码是有损编码。目前使用较多的矢量量化编码方案主要是随机型矢量量化，包括变换域矢量量化；有限状态矢量量化，地址矢量量化，波形增益矢量量化，分类矢量量化及预测矢量量化等。
6.变换编码
变换编码就是将图象光强矩阵时域信号，变换到系数空间频域信号，上进行处理的方法。在空间上具有强相关的信号，反映在频域上是某些特定的区域内能量常常被集中在一起，或者是系数矩阵的分布具有某些规律。我们可以利用这些规律在频域上减少量化比特数，达到压缩的目的。由于正交变换的变换矩阵是可逆的且逆矩阵与转置矩阵相等，这就使解码运算是有解的且运算方便，因此运算矩阵总是选用正交变换来做。常用的变换编码有K，L变换编码和DCT编码。K，L变换编码在压缩比上优于DCT编码，但其运算量大且没有快速算法，因此实际应用中广泛采用DCT编码。
7.模型法编码
预测编码、矢量量化编码以及变换编码都属于波形编码，其理论基础是信号理论和信息论，其出发点是将图象信号看作不规则的统计信号，从象素之间的相关性这一图象信号统计模型出发设计编码器。而模型编码则是利用计算机视觉和 计算机图形学的知识对图象信号的分析与合成。
模型编码将图象信号看作三维世界中的目标和景物投影到二维平面的产物，而对这一产物的评价是由人类视觉系统的特性决定的。模型编码的关键是对特定的图象建立模型，并根据这个模型确定图象中景物的特征参数，如运动参数、形状参数等。解码时则根据参数和已知模型用图象合成技术重建图象。由于编码的对象是特征参数，而不是原始图象，因此有可能实现比较大的压缩比。模型编码引入的误差主要是人眼视觉不太敏感的几何失真，因此重建图象非常自然和逼真。
此外，近些年来；分形编码编码和小波变换的技术也越来越多的应用在图像压缩的领域中，但是大多仍处于研究阶段，常见的图像压缩方法仍以前面介绍的为主。当然，在实际的应用中，多种图像压缩方法往往是结合起来使用的，如JPEG等。
附录3 毕业设计任务书
（基于自组织神经网络的图像压缩编码）
一、毕业设计目的
毕业设计是学生对所学知识进行深化，拓宽，综合运用的重要过程；是对学生学习，研究和实践成果的全面总结。大学生在校学习期间已经按照教学计划的规定，完成了对公共课，基础课，专业课以及选修课等的学习，毕业设计是让学生利用这些所学知识分析解决问题，从而提高学生的科研能力和工作能力，为进一步的学习和走向工作岗位打好基础。
二、主要内容
基于BP神经网络的图像压缩编码中的网络设计和训练以及通过与小波变换的图像压缩编码之后的重建图像进行比较是本次课程设计的核心内容，通过峰值信噪比和压缩率的比较找出原因和不足之处。
三、重点研究问题
BP神经网络在图像压缩时的功能和作用。图像压缩编码技术的应用。
四、主要技术指标或主要参数
网络建立、网络训练，峰值性噪比，压缩率。
五、基本要求
1.翻译外文资料，要求不少于2000字
2.完成对自组织神经网络的图像压缩编码系统的设计。
3.编写MATLAB程序进行仿真。
4.提交正文在15000字以上毕业设计说明书，要求格式规范，文字叙述严谨流畅，图形图表清晰美观，程序编码简单明了，正文中应包括目录、中英文摘要、序言、研究内容、存在问题、进一步改进的工作、参考文献等。
六、其它（包括选题来源）
第3周： 查阅相关资料，完成开题报告
第4-5周 ： 外文文献翻译
第6周： 构思MATLAB程序设计流程，初步完成程序的设计
第7-8周： 优化程序，修改程序错误，完成系统的仿真设计
第9-10周： 撰写论文
第11-12周： 设计ppt，打印论文，答辩
指导教师： 年 月 日
附录4 华北水利水电大学本科生毕业设计开题报告
|
学生姓名 |
牛兆华 |
学号 |
201215701 |
专业 |
通信工程 |
|
题目名称 |
基于自组织神经网络的图像压缩编码 |
||||
|
课题来源 |
自选 |
||||
|
研究或设计概述
|
首先介绍了图像压缩编码的背景和图像压缩编码的必要性。之后介绍了图像压缩编码的基础和图像压缩编码的评价标准。基于BP神经网络的图像压缩编码的思路、流程、方法等。最后通过MATLAB编程实现基于BP神经网络的图像压缩编码。通过图像数据预处理、网络建立和训练、仿真、图像重建四个步骤对图像进行压缩处理，然后利用输入与重建图像的信噪比和峰值信噪比两个性能函数来评定图像压缩的质量，当信噪比和峰值信噪比越大时，表明图像压缩质量越好，图像失真较小。并利用压缩比和比特率两个性能函数来评价压缩性能。压缩比较大，并且压缩重建后的图像失真较小，说明该压缩方法性能较好。经过运用两种方法对图像进行压缩实验，我门可以看出，BP 网络算法、小波压缩算法都能比较好的进行图像压缩运算。 |
||||
|
主 要 内 容 |
日常生活中，图片所占的储存空间很大，不便于拷贝可传输，为我们带来极大的不便。因此，图像压缩所解决的问题就是尽量减少表示数字图像时所需要的数据量。其原理就是去除其中多余的数据，这种变换在图像存储或者传输之前进行，被称为图像的压缩。那么什么是编码呢？这种压缩的方式从数学观点来看，如果我们将一张数字图像看成是由一个个的像素点组成的，那么图像压缩就是将一个个的二维像素阵列变换为一个在统计上无关联的数据集合。 BP神经网络是一种比较成熟的用于图像压缩的神经网络。 本次毕业设计采用的神经网络是BP神经网络，首先对图像进行预处理，之后采用MATLAB神经网络工具箱中提供的函数建立BP神经网络模型并对其进行训练。训练结束后进行图像的压缩和重建。之后又使用基于小波变换的图像压缩编码所得到的结果跟基于BP神经网络的图像压缩编码所得到的结果进行对比，发现设计的不足之处，并分析原因。 |
||||
|
采取的主要技术路线或方法 |
1.BP神经网络的设计和训练。神经网络的设计用MATLAB神经网络函数库的feedforwardnet函数。通过设置训练次数，目标误差等参数建立最基础的BP神经网络。之后调用train函数新建的神经网络进行训练。 2.解释基于小波变换的图像压缩编码的具体含义以及思想，设计出基于小波变换的图像压缩编码的MATLAB程序。 3.使用同一张图片分别进行基于BP神经网络的图像压缩和基于小波变换的图像压缩实验。分别得到两种经过以上两种方法之后的重建图像。 4.通过对重建图像的比对，发现不足之处。 5.MATLAB方法，主要用于后期的图像压缩编码的程序设计。 |
||||
|
时间安排 |
第3周： 查阅相关资料，完成开题报告 第4周 ： 外文文献翻译 第5-6周： 构思MATLAB程序设计流程，初步完成程序的设计 第7-8周： 优化程序，修改程序错误，完成系统的仿真设计 第9-10周： 撰写论文 第11-13周： 设计ppt，打印论文，答辩 |
||||
|
参考文献 |
参考文献 [1] 张徳丰，《MATLAB神经网络应用设计》（第二版）机械工业出版社. [2] 陈明 等著，《MATLAB神经网络原理与实例精解》，清华大学出版社. [3] 张徳丰，《MATLAB数字图像处理》（第二版）机械工业出版社， [4] 张春田，张静著，《数字图像压缩编码》。清华大学出版社. [5] 《关于图像压缩编码算法研究的综述》，王向阳，烟台师范学院学报(自然科学版). [6] 张丽英，提升框架下整数小波变换结合VQ图像压缩方法的研究;吉林大学;2004年. [7] 陈明，《MATLAB函数功能速查效率手册》电子工业出版社. [8] 杨晓华，孔令泉《MATLAB权威指南》.机械工业出版社，,2013年第一版 [9] 李俊山，李旭辉《数字图像处理》（第二版）清湖大学出版社， [10] 罗强 著，《图像压缩编码方法》。西安电子科技大学出版社. |
||||
|
指导教师意见 |
签名： 年 月 日 |
||||
|
备注 |
|
||||
附录5 部分源程序
基于BP神经网络的图像压缩与解压缩MATLAB源程序
% bp_imageCompress.m
% 基于BP神经网络的图像压缩
%% 清理
clc
clear all
rng(0)
%% 压缩率控制
K=4;
N=2;
row=256;
col=256;
%% 数据输入
I=imread('d:\lena.bmp');
% 统一将形状转为row*col
I=imresize(I,[row,col]);
%% 图像块划分，形成K^2*N矩阵
P=block_divide(I,K);
%% 归一化
P=double(P)/255;
%% 建立BP神经网络
net=feedforwardnet(N,'trainlm');
T=P;
net.trainParam.goal=0.001;
net.trainParam.epochs=500;
tic
net=train(net,P,T);
toc
%% 保存结果
com.lw=net.lw{2};
com.b=net.b{2};
[~,len]=size(P); % 训练样本的个数
com.d=zeros(N,len);
for i=1:len
com.d(:,i)=tansig(net.iw{1}*P(:,i)+net.b{1});
end
minlw= min(com.lw(:));
maxlw= max(com.lw(:));
com.lw=(com.lw-minlw)/(maxlw-minlw);
minb= min(com.b(:));
maxb= max(com.b(:));
com.b=(com.b-minb)/(maxb-minb);
maxd=max(com.d(:));
mind=min(com.d(:));
com.d=(com.d-mind)/(maxd-mind);
com.lw=uint8(com.lw*63);
com.b=uint8(com.b*63);
com.d=uint8(com.d*63);
save comp com minlw maxlw minb maxb maxd mind
% bp_imageRecon.m
%% 清理
clear,clc
close all
%% 载入数据
col=256;
row=256;
I=imread('d:\lena.bmp');
load comp
com.lw=double(com.lw)/63;
com.b=double(com.b)/63;
com.d=double(com.d)/63;
com.lw=com.lw*(maxlw-minlw)+minlw;
com.b=com.b*(maxb-minb)+minb;
com.d=com.d*(maxd-mind)+mind;
%% 重建
for i=1:4096
Y(:,i)=com.lw*(com.d(:,i)) +com.b;
end
%% 反归一化
Y=uint8(Y*255);
%% 图像块恢复
I1=re_divide(Y,col,4);
%% 计算性能
fprintf('PSNR :\n ');
psnr=10*log10(255^2*row*col/sum(sum((I-I1).^2)));
disp(psnr)
a=dir();
for i=1:length(a)
if (strcmp(a(i).name,'comp.mat')==1)
si=a(i).bytes;
break;
end
end
fprintf('rate: \n ');
rate=double(si)/(256*256);
disp(rate)
figure(1)
imshow(I)
title('原始图像');
figure(2)
imshow(I1)
title('重建图像');
函数文件re_divide.m
function I=re_divide(P,col,K)
% I=re_divide(P)
% P: K^2*N matrix
% example:
% I=re_divide(P);
% I=uint8(I*255);
% imshow(I)
% 计算大小
[~,N]=size(P);
m=sqrt(N);
% 将向量转为K*K矩阵
b44=[];
for k=1:N
t=reshape(P(:,k),K,K);
b44=[b44,t];
end
% 重新排布K*K矩阵
I=[];
for k=1:m
YYchonggou_ceshi1=b44(:,(k-1)*col+1:k*col);
I=[I;YYchonggou_ceshi1];
end
函数文件block_divide.m
function P = block_divide(I,K)
% P=block_divede(I)
% [row,col]=size(I),row%K==0, and col%K==0
% divide matrix I into K*K block,and reshape to
% a K^2*N matrix
% example:
% I=imread('lena.jpg');
% P=block_divide(I,4);
% 计算块的个数：R*C个
[row,col]=size(I);
R=row/K;
C=col/K;
% 预分配空间
P=zeros(K*K,R*C);
for i=1:R
for j=1:C
% 依次取K*K 图像块
I2=I((i-1)*K+1:i*K,(j-1)*K+1:j*K);
% 将K*K块变为列向量
i3=reshape(I2,K*K,1);
% 将列向量放入矩阵
P(:,(i-1)*R+j)=i3;
end
end
基于小波变换的图像压缩编码MATLAB源程序如下：
clear all;
load wbarb;
subplot(2,2,1);
A=imread('G:\BPYaSuo\lena.bmp');
image(A);
I2=im2double(A);
colormap(map);
xlabel('a)原始图像');
axis square;%产生坐标系
disp('压缩前图像的大小:');
whos('I2')
[c,s]=wavedec2(A,2,'bior3.7');
%对图像用小波进行分解
cal=appcoef2(c,s,'bior3.7');
%提取小波分解结构中的一层低频系数和高频系数
ch1=detcoef2('h',c,s,1);%水平方向
cv1=detcoef2('v',c,s,1);%垂直方向
cv1=detcoef2('d',c,s,1);%对角方向
a1=wrcoef2('a',c,s,'bior3.7',1);%重构低频分量
h1=wrcoef2('h',c,s,'bior3.7',1);%重构水平分量
v1=wrcoef2('v',c,s,'bior3.7',1);%重构垂直分量
d1=wrcoef2('d',c,s,'bior3.7',1);%重构对角分量
c1=[a1,h1,v1,d1];%各频率成分重构
subplot(2,2,2);
image(c1);
axis square;
xlabel('b)分解后低频和高频信息');
%进行图像压缩，保留小波分解第一层低频信息，首先对第一层信息进行量化编码
ca1=appcoef2(c,s,'bior3.7',1);%提取小波分解结构中的一层低频系数和高频系数
ca1=wcodemat(ca1,440,'mat',0);%对矩阵进行伪彩色编码
ca1=0.5*ca1;
subplot(2,2,3);
image(ca1);
colormap(map);%获取当前色图
axis square;
xlabel('c)第一次压缩图像');
disp('第一次压缩图像的大小为:');
whos('ca1')
ca2=appcoef2(c,s,'bior3.7',2);
%保留小波分解第二层低频信息进行压缩
ca2=wcodemat(ca2,440,'mat',0);
%首先对第二层信息进行量化编码
ca2=0.25*ca2;
%改变图像高度并显示
subplot(2,2,4);image(ca2);
colormap(map);
axis square;
xlabel('d)第二次压缩图像');
disp('第二次压缩图像的大小为:');
whos('ca2')
承担因您的行为而导致的法律责任，
本站有权保留或删除有争议评论。
参与本评论即表明您已经阅读并接受
上述条款。